Menelaus of Alexandria was a Greek astronomer, scientist, and mathematician who lived around 100 CE. Menelaus made a significant and lasting contribution to the fields of astronomy, geometry, and trigonometry. His major work, the Spherics survives and presents what is today called Menelaus' Theorem. The theorem uses lettered diagrams of pure geometry to calculate spherical triangles or distances across a sphere with implications for the practical study of astronomy such as the trajectory of planets. Menelaus, and others like him, reduced the physical world to a purely geometric one, and so he was then able to calculate the unmeasurable, an approach which became the very foundation of modern science.
Life & Works
History is almost totally silent regarding any biographical details of Menelaus. All that we do know is that he made a series of astronomical observations in Rome in 98 CE and that he was known to the Greek writer Plutarch (c. 45-50 CE - c. 120-125 CE). We also know the titles of several of his works, mostly via references in the works of others, notably later Arab writers and compilers of (now mostly lost) ancient texts. These works include:
- Spherics (Sphaerica) - Menelaus' most important work, which survives as an Arabic translation. It deals with the mathematical studies of spheres and the implications thereof on the subject of astronomy. The work is divided into three books, the first of which examines spherical triangles, defining them and proposing theorems based on the 4th-3rd century BCE Greek mathematician Euclid's work on plain triangles. This is the earliest surviving detailed study of spherical triangles. The second book concerns spherical topics with observations on astronomy similar to those made by Euclid and the astronomer and mathematician Theodosius of Bithynia (l. c. 100 BCE). The third book is a much more innovative treatise on the fundamental principles of spherical trigonometry, again, the earliest known such study. It presents Menelaus' Theorem (see below) and the Rule of Four Quantities and the Law of Tangents.
- Specific Gravities - another surviving work in Arabic translation. This book was dedicated to the Roman emperor Domitian (r. 81-96 CE).
- Elements of Geometry - three books mentioned by the Persian scholar al-Biruni (b. 973 CE) and likely a collection of problems concerning Euclidean geometry.
- A treatise on chords in a circle, possibly some form of early trigonometric table. This work is referred to by the 4th-century CE mathematician and commentator Theon of Alexandria.
- A work on the signs of the zodiac, which is referred to by the 4th-century CE mathematician Pappus of Alexandria.
- Three works mentioned in the 10th-century CE Fihrist, an Arabic catalogue by Ibn al-Nadim. These are Book on the Triangle, On the Knowledge of the Weights and the Distribution of Different Bodies, and an untitled work on mechanics. These texts possibly included Menelaus' estimation of the precession of the equinoxes.
Menelaus' Theorem
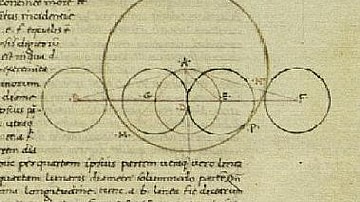
Menelaus is perhaps most famous today for his theory now known as Menelaus' Theorem. Some scholars suggest that the theorem may not have been original and that it had already been proposed by earlier mathematicians but Menelaus' work remains the first known reference to it. The theory involves using a spherical quadrilateral (essentially a lettered diagram) to calculate the shortest curved distances between two points on a sphere. These calculations thus solved the trigonometry problem of how to measure spherical triangles which are formed by three arcs of great circles on a sphere's surface. Menelaus also pioneered the use of great circles (orthodromes), which are circles which intersect a sphere and cross through its centre point, for example, as the equator of the earth does. The mathematician used the arcs of these great circles for his calculations rather than the arcs of parallel circles (for example, the lines of the latitude of the earth) used by his predecessors.
The theorem had consequences for the study of astronomy as the points in the lettered diagram could represent physical objects such as planets. For those readers with a mathematical mind, the Encyclopedia Britannica gives the following succinct explanation of the theory in mathematical terms:
The form of this theorem for plane triangles was expressed as follows: if the three sides of a triangle are crossed by a straight line (one of the sides is extended beyond its vertices), then the product of three of the nonadjacent line segments thus formed is equal to the product of three other line segments.
The theorem was influential in mathematics as it became the foundation for the 2nd-century CE mathematician Claudius Ptolemy's work on spherical astronomy and is noted in his Almagest. Menelaus' Theorem also had an influence on Muslim astronomers prior to 1000 CE. In short, Menelaus had helped in the progress of science by his, and other mathematicians like him, reduction of the physical (for example, planets) to the purely geometrical (for example, mathematical diagrams, theorems and formulaic phrases). Scientists, engineers, and architects could then apply these calculations to the physical world around them. In recognition of his contribution to astronomy, a crater on the Moon has been named after Menelaus.